2023年最後の記事を作成しました！

　こんばんは。

　ブログを執筆をしていたら、23時を回ってしまいました。

　本日書いた記事はこちら。

　「三角錐数」という、ピタゴラス由来の「三角数」の立体バージョンです。

　一般項を求めるための証明、面白い性質の紹介などで記事を作成するつもりでしたが、書き始めると別証明を思いついたり、歴史について語ったりとなかなかの分量となってしまいました。

　個人的に面白いなと思ったのが、パスカルの三角形の中に三角錐数が出てくること。

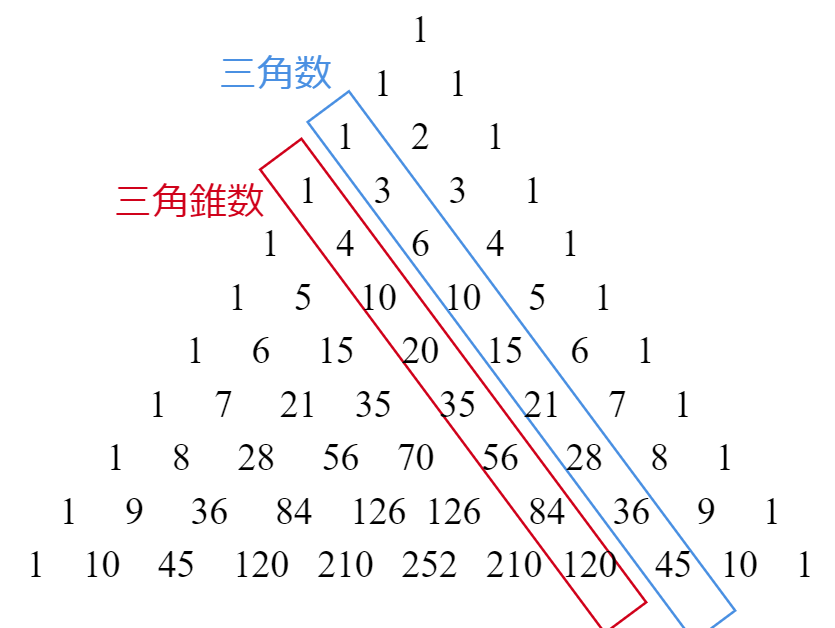
　パスカルの三角形自体は、11世紀頃から存在するものの、パスカルの研究熱がすごく、いろいろな発見をしたため彼の名を冠しています。（オマル・ハイヤームや楊輝、残念‥‥）

　文通相手のフェルマーとこの三角形を共有した際、フェルマーがツンデレな感じで、パスカルを自分の沼に引きずり込もうとしているのがおもしろい。

　そのあたりのエピソードも含めて、三角錐数の記事を書きましたので、是非ご覧ください。

　$~2024~$が偶数の２乗の和で表される理由もわかります！

2024=2^2+4^2+6^2+\cdots+22^2

Fukusukeの数学めも

三角錐数は三角数を重ねた数列！その一般項や美しい性質を解説！ | Fukusukeの数学めも この記事では、三角錐数に関する数学的概念を解説しています。三角数を基にした三角錐数の定義、それらの数の特徴、一般項の導出方法、そして奇数番目と偶数番目の三角錐数…

　2024年に向け、良いお年をお迎えください。